Are We Willing to Question the Content We Teach?

It is pretty hard to be a convincing and effective teacher without believing in the content. But most teachers can probably relate to that feeling of "I have way too much to teach and not enough time to teach it." Not only do I get that feeling, but I also find myself wondering why we try to teach so much content. As a math teacher, I hope that my students will gain the ability to think critically and analyze problems. Everything I teach goes back to that goal. Let me give you and example of content I find extremely beneficial and engaging as well as an example of content that I believe does not help students gain the skills we hope they will gain when learning math.


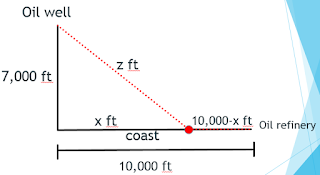
An offshore oil well is situated in the ocean 7,000 feet from the nearest point (point A) on a straight coastline. An oil refinery is located 10,000 feet down the coast from point A. Laying pipe under water costs $16/foot and laying pipe on land costs $7/foot. The engineers want to find the path that will minimize the cost of laying pipe from the oil well to the refinery.

I love questions like this. Though there are many questions we can ask about this scenario, I pulled this from an activity involving optimization problems. That is one of the obvious questions: how much pipe should be laid under water and how much pipe should be laid on land if the company wants to minimize the cost of the job? To answer this question, students will usually have to draw a picture, label the picture, do some algebra, and depending on the complexity of the functions involved, they may even utilize technology to find their final answer. 

The cost of laying pipe on land will be 7 dollars per foot multiplied by 10,000 - x ft, where x is whatever distance the pipe will strike down coast from the oil well. The cost in water will be 16 dollars per foot multiplied by z feet. But now we have three variables (the cost of the job, which depends on z feet of pipe in water and (10,000-x) feet of pipe on land), so the students have to figure out how to eliminate one. Applying the Pythagorean Theorem to the right triangle yields:

                  So then the cost of the pipe in water would be 16 dollars per foot multiplied by



Now we can plug the cost function into desmos or a graphing calculator to find the minimum cost.

Okay, not quite done yet. Now they have to interpret what that minimum point means. This graph represents the cost of the job given different x distances. If the pipe hits the coast 3,405.735 feet down the coast from the oil well, the job will cost $170,712.46, the minimum cost. 

The other great thing about this problem is I could post it on twitter or send it out in an email to my colleagues and different teachers could come up with hundreds of extensions to make this problem deeper and more rich. 

Now, let me give you an example of a concept that I have disliked teaching. 

Circles have a pretty simple definition. It's just the set of all points that are an equal distance away from a given center. Interesting properties start showing up when drawing lines through circles that form angles. The angles could be inside the circle, outside of the circle, or on the circle. Let's looks at a diagram where the angle is outside of the circle. 

It turns out that the measure of angle A is equal to half of the difference of the measure of the arc ED and the measure of the arc BC (do not confuse measure and length. Length is a distance, but we are talking about degrees here). 

We could go through the proof. There are also ways to make students think a little harder about this property. But really, this is level one information. Students are often asked to memorize properties like this and apply them to simple problems. Problems like this may even show up on important standardized tests (like the SAT or ACT). But I haven't found a way to meaningfully work through this concept while helping my students develop their critical thinking and ability to analyze problems. It's not a very applicable concept and it is hard to sell to them. What happens instead is that students memorize the different properties and forget them as soon as possible. I mean, can you even remember the property now, even just a paragraph later? 

The answer to this issue for now is knowing exactly what we can spend more time on and what we can gloss over, which really good teachers are able to do effectively. However, as long as we are restricted by the long list of objectives we are expected to get through, we will not always have time to get in depth with problems like the first example. The danger is we end up half teaching everything. When we are half teaching, the students might as well not even be learning. We feel like we are just getting by, they feel like they are just getting by, and very little authentic learning is actually occurring. 

Students are begging for relevance. They ask us constantly "why are we learning this?" My answer, as well as other math educators' answer, is usually "you are exercising your brain. You are problem solving. You are thinking critically. Hopefully you will have a job one day that makes you do all of those things, and you will be better prepared for that by learning math." If we give them that answer, everything we teach should help students work towards that goal. And if something we are teaching isn't really working towards that goal, then what is the point?

I love math. I love all of it. I think it is amazing and beautiful and really cool. But I'm also willing to question the importance of everything in my curriculum. Many students will likely not gain an appreciation for all of math in 12 years of education. But we can cut down on what we are teaching and help them appreciate a subset of what we are currently trying to teach. We can get more in depth so that students can authentically learn instead of feeling like they are faking it until they graduate. As long as the current list of objectives are in place with little wiggle room, many students will continue to feel left behind while we continue to feel like we are rushing through everything.